Survival with a Regression Spline
By popular request, here’s an example using a piecewise exponential model with a regression spline, applied to the recidivism data. The first thing to do is read the data and create a failure indicator.
. use https://www.stata.com/data/jwooldridge/eacsap/recid.dta, clear . gen fail = 1 - cens
> library(haven)
> recid <- read_dta("https://www.stata.com/data/jwooldridge/eacsap/recid.dta")
> recid$fail <- 1 - recid$cens
> nrow(recid)
[1] 1445
Next I will split the data every three months, and create a new variable to reflect exposure (time lived in each interval)
. gen id = _n
. stset durat, fail(fail) id(id)
Survival-time data settings
ID variable: id
Failure event: fail!=0 & fail<.
Observed time interval: (durat[_n-1], durat]
Exit on or before: failure
──────────────────────────────────────────────────────────────────────────
1,445 total observations
0 exclusions
──────────────────────────────────────────────────────────────────────────
1,445 observations remaining, representing
1,445 subjects
552 failures in single-failure-per-subject data
80,013 total analysis time at risk and under observation
At risk from t = 0
Earliest observed entry t = 0
Last observed exit t = 81
. stsplit trimester, at(3(3)78)
(25,750 observations (episodes) created)
> library(survival) > recidx <- survSplit(Surv(durat, fail) ~ ., cut=seq(3,78,3), data=recid) > nrow(recidx) [1] 27195 > recidx$exposure <- recidx$durat - recidx$tstart
To model the baseline hazard I will use a regression spline with internal knots at 30, 40 and 60 weeks. These are approximately the quartiles of overall survival as calculated using Kaplan-Meier. To define the spline I used the mid-point of each interval, 1.5 months after the start. I then fit a Poisson model with the log of exposure as an offset
. gen mid = _t0 + 1.5
. bspline, xvar(mid) knots(0 30 40 60 80) p(3) gen(bspl)
. gen expo = _t - _t0
. poisson _d bspl* workprg priors tserved felon drugs black married ///
> educ age, exposure(expo) nocons
Iteration 0: log likelihood = -39499.985
Iteration 1: log likelihood = -2902.2437
Iteration 2: log likelihood = -2828.6165
Iteration 3: log likelihood = -2804.828
Iteration 4: log likelihood = -2804.7856
Iteration 5: log likelihood = -2804.7856
Poisson regression Number of obs = 27,195
Wald chi2(16) = 12472.26
Log likelihood = -2804.7856 Prob > chi2 = 0.0000
─────────────┬────────────────────────────────────────────────────────────────
_d │ Coefficient Std. err. z P>|z| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
bspl1 │ -10.76743 3.01364 -3.57 0.000 -16.67406 -4.860806
bspl2 │ -2.446414 .7114559 -3.44 0.001 -3.840841 -1.051986
bspl3 │ -4.048105 .3876143 -10.44 0.000 -4.807815 -3.288395
bspl4 │ -4.701796 .383244 -12.27 0.000 -5.452941 -3.950652
bspl5 │ -4.827016 .5760656 -8.38 0.000 -5.956084 -3.697948
bspl6 │ -5.630131 1.271756 -4.43 0.000 -8.122728 -3.137534
bspl7 │ -13.58216 12.08349 -1.12 0.261 -37.26537 10.10105
workprg │ .0529768 .0903916 0.59 0.558 -.1241876 .2301411
priors │ .0949319 .0134198 7.07 0.000 .0686297 .1212342
tserved │ .0123086 .0016645 7.39 0.000 .0090462 .0155711
felon │ -.3046545 .104908 -2.90 0.004 -.5102704 -.0990386
drugs │ .2639392 .0979932 2.69 0.007 .0718761 .4560023
black │ .393758 .0876149 4.49 0.000 .2220359 .56548
married │ -.1347573 .1090351 -1.24 0.216 -.3484622 .0789475
educ │ -.0197291 .019438 -1.01 0.310 -.0578269 .0183686
age │ -.003322 .0005175 -6.42 0.000 -.0043362 -.0023078
ln(expo) │ 1 (exposure)
─────────────┴────────────────────────────────────────────────────────────────
> library(splines)
> mf <- fail ~ offset(log(exposure)) + workprg + priors + tserved + felon +
+ drugs + black + married + educ + age + bs(tstart + 1.5, knots=c(30, 40, 60))
> pwe <- glm(mf, family=poisson, data=recidx)
> coef(summary(pwe))[1:10,]
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.032652566 0.3017915359 -13.3623780 1.003077e-40
workprg 0.052976769 0.0903916357 0.5860804 5.578215e-01
priors 0.094931924 0.0134197589 7.0740410 1.504858e-12
tserved 0.012308637 0.0016645485 7.3945799 1.418560e-13
felon -0.304654512 0.1049079755 -2.9040167 3.684085e-03
drugs 0.263939139 0.0979931661 2.6934443 7.071795e-03
black 0.393757912 0.0876148714 4.4941904 6.983513e-06
married -0.134757315 0.1090350844 -1.2359078 2.164928e-01
educ -0.019729166 0.0194379965 -1.0149794 3.101156e-01
age -0.003321962 0.0005174536 -6.4198264 1.364298e-10
You may want to check that the coefficients for our predictors are very similar to those obtained using a Cox model. As for the shape of the hazard, we can predict using the spline coefficients.
. preserve // for safety
. egen tag = tag(mid)
. keep if tag // one obs per interval
(27,168 observations deleted)
. gen shat = 0
. forvalues i=1/7 {
2. quietly replace shat = shat + bspl`i' * _b[bspl`i']
3. }
. expand 2
(27 observations created)
. gen first = _n <= 27
. replace mid = mid - 1.5 if first
(27 real changes made)
. replace mid = mid + 1.5 if !first
(27 real changes made)
. sort mid first
. line shat mid, xtitle(duration)
. graph export pweSpline.png, width(500) replace
file pweSpline.png saved as PNG format
> library(ggplot2)
> m <- seq(1.5, 79.5, 3)
> y <- bs(m, knots=c(30,40,60)) %*% coef(pwe)[11:16]
> xy <- data.frame( duration = sort(c(m-1.5, m+1.5)), hazard = rep(y, rep(2,length(y))))
> ggplot(xy, aes(duration, hazard)) + geom_line()
> ggsave("pweSpliner.png", width=500/72, height=400/72, dpi=72)
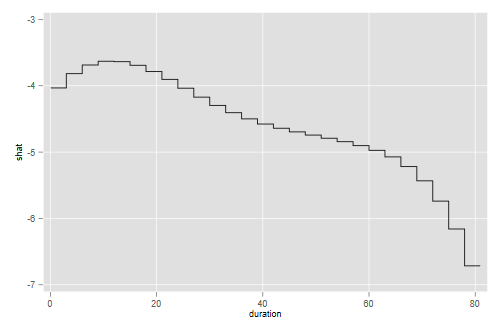
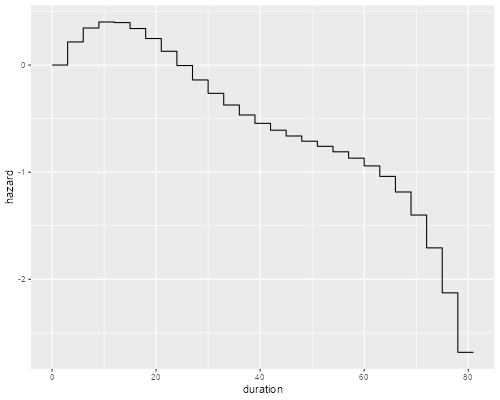
Showing once agan that the hazard appears to rise initially and then decline steadily, so a log-normal is not a bad fit. Note that plotting the spline would be a bit misleading, as we really didn’t fit a curve, but rather a piecewise constant hazard where the value in each three-month interval is taken from the curve. The graph above takes this into account.
