4 November 2017
Let us read the fuel efficiency data that ships with Stata
. sysuse auto, clear (1978 automobile data)
To study how fuel efficiency depends on weight it is useful to
transform the dependent variable from “miles per gallon” to “gallons per 100 miles”
. gen gphm = 100/mpg
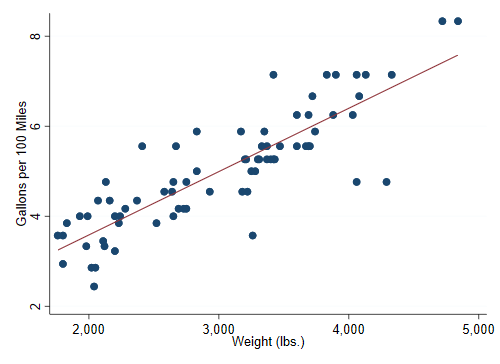
We then obtain a fairly linear relationship
. twoway scatter gphm weight || lfit gphm weight, /// > ytitle(Gallons per 100 Miles) legend(off) . graph export auto.png, width(500) replace file auto.png saved as PNG format

The regression equation estimated by OLS is
. regress gphm weight
Source │ SS df MS Number of obs = 74
─────────────┼────────────────────────────────── F(1, 72) = 194.71
Model │ 87.2964969 1 87.2964969 Prob > F = 0.0000
Residual │ 32.2797639 72 .448330054 R-squared = 0.7300
─────────────┼────────────────────────────────── Adj R-squared = 0.7263
Total │ 119.576261 73 1.63803097 Root MSE = .66957
─────────────┬────────────────────────────────────────────────────────────────
gphm │ Coefficient Std. err. t P>|t| [95% conf. interval]
─────────────┼────────────────────────────────────────────────────────────────
weight │ .001407 .0001008 13.95 0.000 .001206 .0016081
_cons │ .7707669 .3142571 2.45 0.017 .1443069 1.397227
─────────────┴────────────────────────────────────────────────────────────────
Thus, a car that weighs 1,000 pounds more than another requires on average an extra 1.4 gallons to travel 100 miles.
That’s all for now!