Kaplan-Meir Survival
We’ll illustrate the Kaplan-Meier estimator with the classic dataset used by Cox in his seminal paper on proportional hazard models. The data shows the length of remission in weeks for two groups of leukemia patients, treated and controls.
We start by reading the data, available in the datasets section as a
plain text file gehan.dat and a Stata file
gehan.dta.
. use https://grodri.github.io/datasets/gehan, clear
(Dataset used in Cox's 1972 paper, JRSS 34:187-220)
. stset weeks, failure(relapse) // define as survival data
Survival-time data settings
Failure event: relapse!=0 & relapse<.
Observed time interval: (0, weeks]
Exit on or before: failure
──────────────────────────────────────────────────────────────────────────
42 total observations
0 exclusions
──────────────────────────────────────────────────────────────────────────
42 observations remaining, representing
30 failures in single-record/single-failure data
541 total analysis time at risk and under observation
At risk from t = 0
Earliest observed entry t = 0
Last observed exit t = 35
> library(survival)
> library(dplyr)
> library(ggplot2)
> gehan <- read.table("https://grodri.github.io/datasets/gehan.dat")
> summarize(gehan, events = sum(relapse), exposure = sum(weeks))
events exposure
1 30 541
As you can see, 30 of the 42 patients had a relapse, with a total exposure time of 541 weeks. The weekly relapse rate is 7.8%.
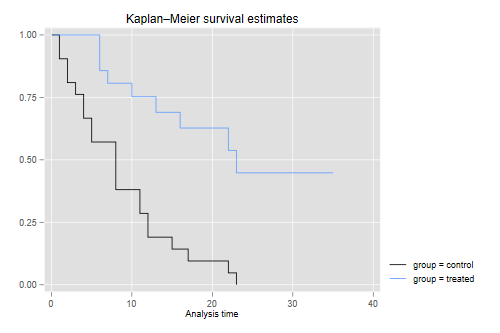
Next we compute and plot the Kaplan-Meir estimator of the survival function in each of the two groups.
. sts graph, by(group)
Failure _d: relapse
Analysis time _t: weeks
. graph export kmg.png, width(500) replace
file kmg.png saved as PNG format
> kmg <- survfit(Surv(weeks, relapse) ~ group, data=gehan)
> #plot(kmg)
> a = 1:kmg$strata[1]
> kmdf <- data.frame(group = rep(c("control", "treated"), kmg$strata+1),
+ time = c(0, kmg$time[a], 0, kmg$time[-a]),
+ surv = c(1, kmg$surv[a], 1, kmg$surv[-a])) %>% group_by(group)
> ggplot(kmdf, aes(time, surv, color=group)) + geom_step()
> ggsave("kmgr.png", width=500/72, height=400/72, dpi=72)
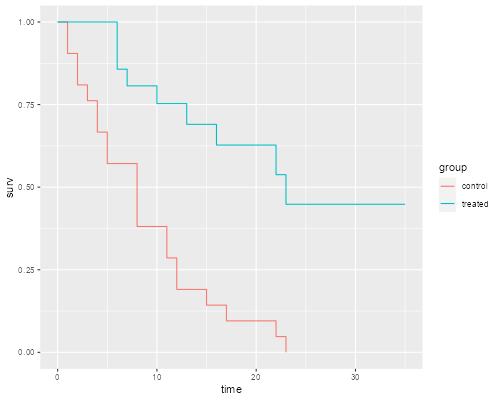
The graph shows that after 23 weeks all patients in the control group had relapsed, but about half those in the treated group remained in remission. We can list the survival function.
. sts list, by(group)
Failure _d: relapse
Analysis time _t: weeks
Kaplan–Meier survivor function
By variable: group
At Net Survivor Std.
Time risk Fail lost function error [95% conf. int.]
────────────────────────────────────────────────────────────────────────
control
1 21 2 0 0.9048 0.0641 0.6700 0.9753
2 19 2 0 0.8095 0.0857 0.5689 0.9239
3 17 1 0 0.7619 0.0929 0.5194 0.8933
4 16 2 0 0.6667 0.1029 0.4254 0.8250
5 14 2 0 0.5714 0.1080 0.3380 0.7492
8 12 4 0 0.3810 0.1060 0.1831 0.5778
11 8 2 0 0.2857 0.0986 0.1166 0.4818
12 6 2 0 0.1905 0.0857 0.0595 0.3774
15 4 1 0 0.1429 0.0764 0.0357 0.3212
17 3 1 0 0.0952 0.0641 0.0163 0.2612
22 2 1 0 0.0476 0.0465 0.0033 0.1970
23 1 1 0 0.0000 . . .
treated
6 21 3 1 0.8571 0.0764 0.6197 0.9516
7 17 1 0 0.8067 0.0869 0.5631 0.9228
9 16 0 1 0.8067 0.0869 0.5631 0.9228
10 15 1 1 0.7529 0.0963 0.5032 0.8894
11 13 0 1 0.7529 0.0963 0.5032 0.8894
13 12 1 0 0.6902 0.1068 0.4316 0.8491
16 11 1 0 0.6275 0.1141 0.3675 0.8049
17 10 0 1 0.6275 0.1141 0.3675 0.8049
19 9 0 1 0.6275 0.1141 0.3675 0.8049
20 8 0 1 0.6275 0.1141 0.3675 0.8049
22 7 1 0 0.5378 0.1282 0.2678 0.7468
23 6 1 0 0.4482 0.1346 0.1881 0.6801
25 5 0 1 0.4482 0.1346 0.1881 0.6801
32 4 0 2 0.4482 0.1346 0.1881 0.6801
34 2 0 1 0.4482 0.1346 0.1881 0.6801
35 1 0 1 0.4482 0.1346 0.1881 0.6801
────────────────────────────────────────────────────────────────────────
Note: Net lost equals the number lost minus the number who entered.
> summary(kmg)
Call: survfit(formula = Surv(weeks, relapse) ~ group, data = gehan)
group=control
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 21 2 0.9048 0.0641 0.78754 1.000
2 19 2 0.8095 0.0857 0.65785 0.996
3 17 1 0.7619 0.0929 0.59988 0.968
4 16 2 0.6667 0.1029 0.49268 0.902
5 14 2 0.5714 0.1080 0.39455 0.828
8 12 4 0.3810 0.1060 0.22085 0.657
11 8 2 0.2857 0.0986 0.14529 0.562
12 6 2 0.1905 0.0857 0.07887 0.460
15 4 1 0.1429 0.0764 0.05011 0.407
17 3 1 0.0952 0.0641 0.02549 0.356
22 2 1 0.0476 0.0465 0.00703 0.322
23 1 1 0.0000 NaN NA NA
group=treated
time n.risk n.event survival std.err lower 95% CI upper 95% CI
6 21 3 0.857 0.0764 0.720 1.000
7 17 1 0.807 0.0869 0.653 0.996
10 15 1 0.753 0.0963 0.586 0.968
13 12 1 0.690 0.1068 0.510 0.935
16 11 1 0.627 0.1141 0.439 0.896
22 7 1 0.538 0.1282 0.337 0.858
23 6 1 0.448 0.1346 0.249 0.807
The convention is to report the survival function immediately after each time. In the control group there are no censored observations, and the Kaplan-Meier estimate is simply the proportion alive after each distinct failure time. You can also check that the standard error is the usual binomial estimate. For example just after 8 weeks there are 8 out of 21 alive, the proportion is 8/21 = 0.381 and the standard error is v0.381(1 - 0.381)/21) = 0.106.
In the treated group 12 cases are censored and 9 relapse. Can you compute the estimate by hand? The distinct times of death are 6, 7, 10, 13, 16, 22 and 23. The counts of relapses are 3, 1, 1, 1, 1, 1, 1. When there are ties between event and censoring times it is customary to assume that the event occurred first; that is, observations censored at t are assumed to be exposed at that time, effectively censored just after t. The counts of censored observations after each death time (but before the next) are 1, 1, 2, 0, 3, 0 and 5. When the last observation is censored the K-M estimate is greater than zero, and is usually considered undefined after that.
